Our article “Optimized correlations inspired by perturbation theory” is now published: https://doi.org/10.1103/PhysRevB.99.19515
In the article we derive a simple approximation of the pair distribution function, which performs particularly well for the strongly correlated electron gas. It is the self-consistent solution of two equations:
\(\bigg[-\frac{\hbar^2}{m}\nabla^2 + v(r) + w_{\scriptscriptstyle\mathrm I}(r) +
V_{\scriptscriptstyle\mathrm F}(r)\, \bigg]_{\phantom{\big|}} \sqrt{g(r)} =\, 0 \) *
and
\(\tilde{w}_{\mathrm I}(q)=\, -\frac{\hbar^2 q^2}{4m} \left[\frac{1}{S(q)}-\frac{1}{S_{\mathrm{F}}(q)}\right]^2\left[\frac{2S(q)}{S_{\mathrm{F}}(q)}+1\right]\)
These two equations have a nice physical interpretation, the first eq. approximates the ladder diagrams and the second the ring (or bubble) diagrams. The result for the pair distribution function is shown in the figure below, for more details have a look into the article.
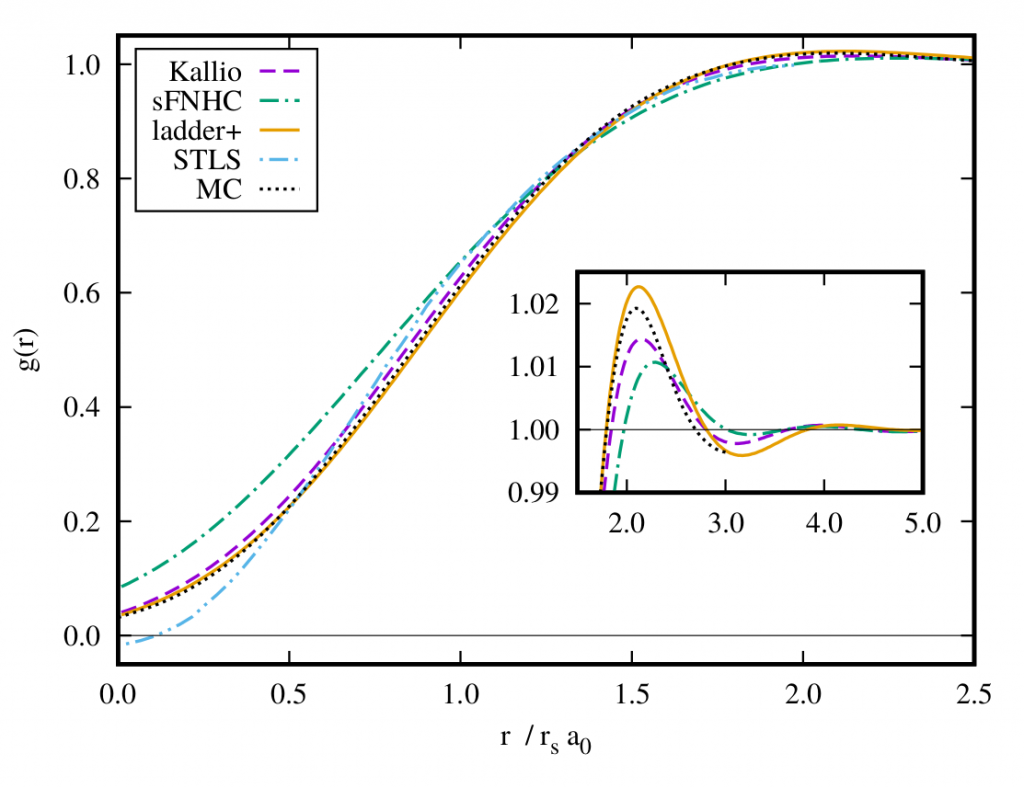
we used the relation \(g(r)-1 = \int \frac{d^3q}{(2\pi)^3\rho} e^{i{\bf q\cdot r}}\, \big(S(q)- 1\big)\).
- *with \(V_{\scriptscriptstyle\mathrm F}\equiv\frac{\hbar^2\nabla^2\sqrt{g_{\scriptscriptstyle\mathrm F}}}{m\sqrt{g_{\scriptscriptstyle\mathrm F}}}\)
